Many-body information and physics

Information in many-body systems #

The spreading of entanglement has been a major research theme in the many-body physics community for several years now. Most recently, a lot of attention has been devoted to the entanglement phase transition that occurs in monitored quantum circuits or when measuring all qubits in the bulk of a state produced in a shallow circuit.

In one line of research, we were wondering how fundamentally “quantum” the measurement-induced phase transition is. To our surprise (at least initially), we numerically found that one can define classical models (cellular automata) that exihibt very similar behaviour [1]. Recently, we made this connection much stronger by introducing and studying models of random reversible classical circuits, for which it is possible to compute certain quantities such as Renyi-2 entanglement growth or out-of-time ordered correlators analytically [2]. Remarkably, we discovered exact mathematical equalities between quantities defined classically (like damage spreading or growth of entropy) to equivalent quantum quantities (OTOCs and also growth of entropy).

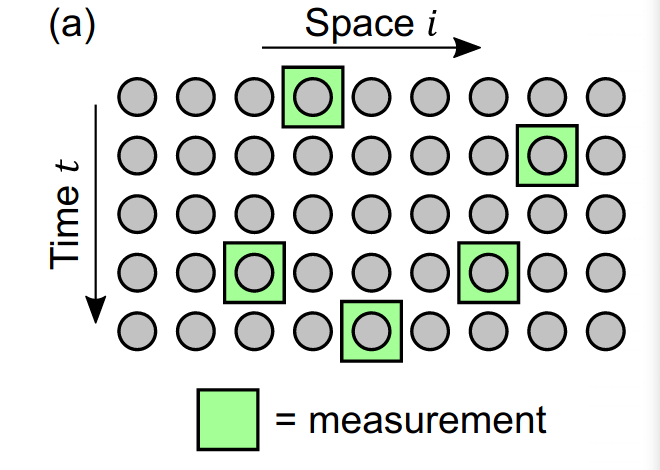
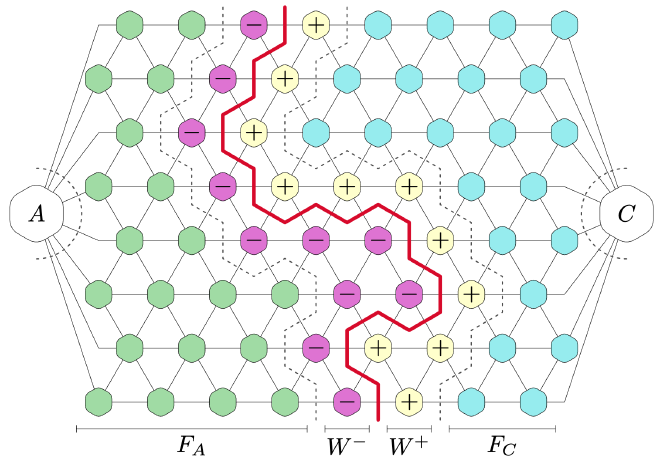
Most recently, we looked at a different form of entanglement transition that has its origins in holography, but that is also closely related to recent demonstrations of quantum computational advantage. In a seminal paper, Hayden et al. showed that random tensor networks obey the Ryu-Takanagi formula, where the entanglement of a boundary region is given by the length of cuts through the bulk. They established this by mapping the formula for the Renyi-2 entropy of a boundary region to the partition function of the Ising model, which at low temperatures is dominated by domain walls that contribute in the same way as the cuts in the Ryu-Takanagi formula. Interestingly, the mechanism behind this is virtually the same as what is known as measurement-induced entanglement (MIE). There, we take a state produced by a shallow-depth circuit (e.g. in 2D), measure all bulk qubits in the computational basis, and consider the ensemble of post-measurement states at the boundaries. It turns out that when the circuit is deep enough, the post-measurement states have volume-law entanglement, but when it is too shallow, the boundary states have area-law entanglement.

It has been (convincingly) conjectured that the transition between these two regimes lies at constant depth. However, a proof has been elusive, because the standard technique (mapping to an Ising model) has approximations that cannot be controlled at constant circuit depth. In our recent paper, we managed to prove that volume-law entanglement is indeed generated in certain classes of random circuits [4]. At the moment our proof works only for one specific circuit depth, so it would still be very nice to extend the proof such that it works for all circuit depths above the constant value we found. Moreover, for technical reasons, we also need to consider qudits of local Hilbert space dimension >133. Hopefully, one day we can extend our result to include qubits!

1. Bridging the gap between classical and quantum many-body information dynamics
   Pizzi, Malz, Nunnenkamp, Knolle, PRB (2022), arXiv
2. Quantum and Classical Dynamics with Random Permutation Circuits
   Bertini, Klobas, Kos, Malz, arXiv (2024)
3. Measurement-induced entanglement and complexity in random constant-depth 2D quantum circuits
   McGinley, Ho, Malz, arXiv (2024)

Computational complexity of tensor network states #

If a state has a low circuit complexity, it is also easy to classically simulate it. Conversely, if a computationally hard problem can be embedded into a state, then it cannot be too easy to prepare it. Complexity is an important notion for variational ansatz states, because if the complexity of a variational family is too low, we cannot use the family to solve hard problems. On the other hand, if it’s too high, we cannot use the family full stop.

Isometry tensor network states, introduced in (Zaletel and Pollmann, 2020) seem to inhabit a sweet spot: they can capture many states, so they aren’t trivial, but they also not too hard. But how hard are they exactly? This is what we set out to answer in Ref. [1]. The key twist in this work is that properties (say, local expectation values) of 2D isoTNS can be mapped to an equivalent (1+1)D open quantum circuit, which lets us map the complexity of local expectation values to simulating quantum circuits with depolarizing noise, and sampling complexity to measurement-induced phase transitions.

1. Computational complexity of isometric tensor network states
   Malz, Trivedi, arXiv

Discrete time crystals #

Time crystals are nonequilibrium phases of matter that spontaneously break time-translation symmetry. The classic example here is one of a spin chain with a π-pulse applied every period. Two π-pulses are equivalent to the identity, which means the systems recurs only after two periods [a].

In a generic closed system, one would expect the drive to heat up the system to a infinite temperature state, which is why it is understood that one needs to add MBL to stabilize the phase [a]. Yet, even in the absence of MBL gives a subharmonic response for time scales that are exponentially long in systems sizes, which would suggest time-crystalline order in the absence of MBL. In a numerical analysis, we have shown that a previously overlooked, subtle effect can explain why the apparent subharmonic response scaling is misleading, thus further clarifying the role of MBL in such systems [1].

In classical systems, it is less clear how time crystalline phases can arise, as also the “rules” are less clear. Previous work has suggested that in one-dimensional systems, short-range interactions are not sufficient [b], but long-range interactions may indeed stabilize DTC order [c]. In our work we take ask more questions about this classical setting, by studying the example of seasonal epidemic spreading on small-world graphs, and identify a setup where an arbitrarily small density of random (infinite-range) bonds is sufficient for a transition to a time-crystalline phase [2]. In contrast to previous models, our model includes non-Markovianity in the form of “immune sites” that are non-dynamical for a set period of time. This opens an interesting parallel between research on DTCs and models that have been in use for decades in epidemiology.

1. Time crystallinity and finite-size effects in clean Floquet systems
   Pizzi, Malz, Nunnenkamp, Knolle, PRB (2020), arXiv.
2. Seasonal epidemic spreading on small-world networks: Biennial outbreaks and classical discrete time crystals
   Malz, Pizzi, Nunnenkamp, Knolle, PRR (2021), arXiv

Topological magnon amplification #

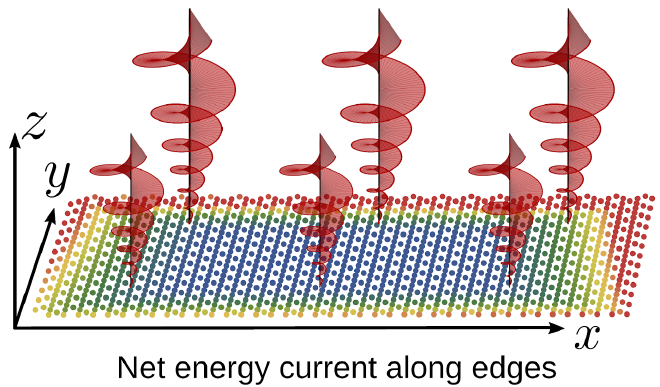
This project concerns the amplification of magnons in chiral topological edge modes [1]. Such modes arise in certain (3D, but effectively 2D) magnetic insulators with Dzyaloshinskii-Moriya interaction, most notably with kagome [e] and honeycomb [f] lattices. We show that driving such systems with light can lead to edge mode instabilities and nonequilibrium steady states with large edge magnon population and further show that driving with a gradient leads to some sort of driven magnon Hall effect, two aspects that will aid their direct experimental detection. Beyond the characterisation these materials, our magnon amplification mechanism can be used to build a coherent magnon source (a magnon laser) and a travelling-wave magnon amplifier, two devices with great potential in the realm of magnon spintronics.

1. Topological magnon amplification
   Malz, Knolle, Nunnenkamp, ncomms (2019), arXiv