Research

My research is motivated and inspired by the rapid development of experimental setups in which many-body quantum systems can be controlled to a high level of precision, allowing one to use them for quantum simulation, computation, or metrology. Here I briefly explain some of the broad topics that were important in my recent work; the links will give you a more detailed idea of my work in the respective field.

For a complete list of publications please refer to arXiv or google scholar.

Tensor network state preparation #

Whether it is computing the time evolution of a system or finding its ground state, state preparation is a key step in many quantum algorithms. We work on this problem predominantly in the context of tensor network states, which constitute a versatile family of states that generally approximate ground states of local Hamiltonians well.

In one dimension, these states are known as MPS, and we have recently proven that essentially all of them (with some asterisks) can prepared very efficiently and also provided an algorithm to do so [2]. In two and higher dimensions, we have introduced an adiabatic path to produce many states including the AKLT state [3], and studied states that can be prepared using sequential circuits and shown that those include many important states such as ground states of many topological models [4], which finds application in preparing entangled photon states [5–7].

In our most recent work, we use what we have learned about sequential circuits to assess the computational complexity of isometric tensor network states (isoTNS) [1]. The key twist in this work is that properties (say, local expectation values) of 2D isoTNS can be mapped to an equivalent (1+1)D open quantum circuit, which lets us map the complexity of local expectation values to simulating quantum circuits with depolarizing noise, and sampling complexity to measurement-induced phase transitions.

Quantum simulation #

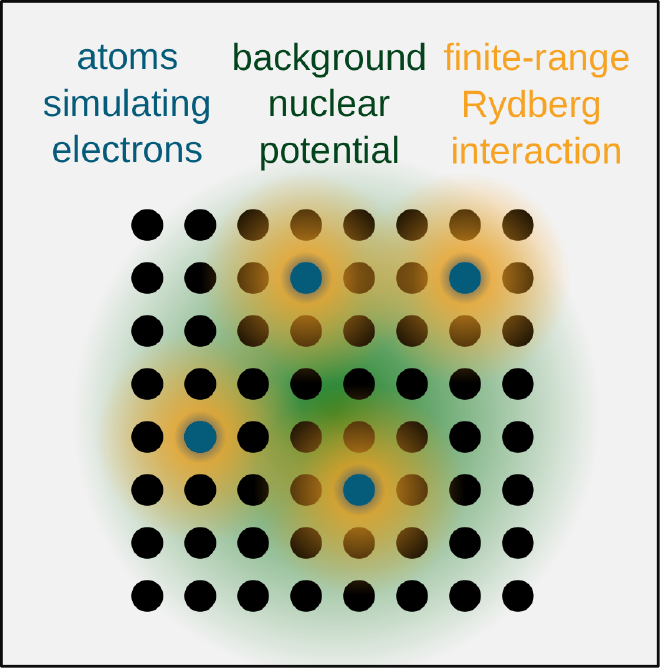
Ref. [10]. Fermionic atoms (blue) move in an optical lattice (black). They are subject to a background potential that mimics nuclei (green) and long-range repulsive interactions generated through Rydberg dressing (yellow).

Atoms in optical lattices is an extremely successful platform for analogue quantum simulation, but essentially all experiments focus on condensed-matter models with local interactions. There are good reasons for this, but we can ask whether it is possible to go beyond. My research research in this field is concerned with finding ways to go beyond this paradigm. On the one hand, this is a technological challenge, and we have explored how one could use subwavelength atomic arrays to achieve long-range interactions [8, 9]. On the other hand, we need to understand what there is to simulate. In this direction, we recently showed that using comparatively simple tools such as Rydberg dressing, one can already simulate very interesting few-body models such as quantum chemistry [10].

Quantum simulation with fully coherent dipole-dipole interactions mediated by three-dimensional subwavelength atomic arrays
Brechtelsbauer, Malz, PRA (2021), arXiv
Atomic waveguide QED with atomic dimers
Castells-Graells, Malz, Rusconi, Cirac, PRA (2021), arXiv
Few-Body Analog Quantum Simulation with Rydberg-Dressed Atoms in Optical Lattices
Malz, Cirac, PRXQ (2023), arXiv

Quantum optics #

In quantum optics, we study the interaction between atoms (or few-level systems in general) with light (a bosonic field). This is a reasonably mature field, and its achievements have paved the way to the astonishing devices we have today. However, there are still open questions, mainly concerning many-body physics in open quantum systems, or how to achieve better control, e.g., through collective effects, as well as to develop protocols to prepare useful states of light.

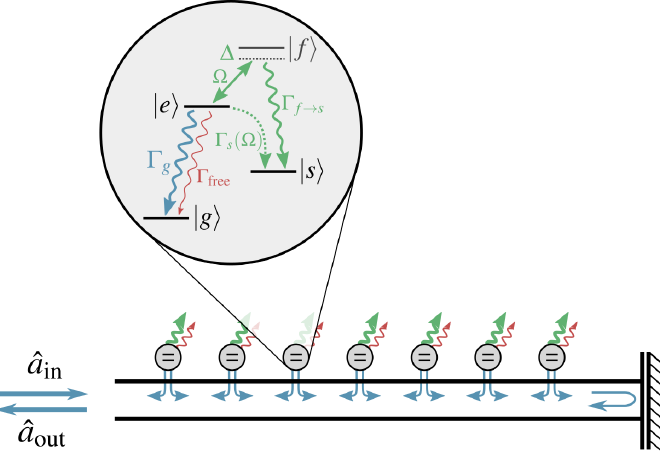
With better ways to control light-matter interactions (for example through subwavelength arrays), we can devise protocols to entangle atoms and photons, and use the intrinsic nonlinearity of atoms to measure, control, and generate non-classical states of light. Under this paradigm, we have shown that a one-dimensional array of atoms coupled to a waveguide (waveguide QED, see figure) makes a robust photon detector [11], and this also inspired us to define a new meterological task that exhibits a quantum advantage [13]. We have also shown that three-dimensional Rydberg arrays can be used to generate entangled photonic states in free space [5, above]. Looking more fundamentally at photon emission, we found an analytical solution to Dicke superradiance and proved rigorously that it converges in the limit of large atom numbers [13] and we explored the novel phenomenology that emerges when emitters are coupled to non-Hermitian baths [14, 15], and contributed to control and understanding of non-Markovian environments [16, 17].

Nonequilibrium many-body physics #

Nonequilibrium many-body physics is a field that draws a lot of inspiration from the development of quantum devices with controllable dynamics. When describing real materials, it is often sufficient to focus on equilibrium properties (or perturbations around equilibrium), but quantum devices, and in particular analogue simulators have made it possible to systematically investigate quench dynamics.

While kicked models have a long history, it was fairly recently that periodic driving of a many-body system can lead to robust subharmonic response in the thermodynamic limit even in closed systems, a phenomenon that has been termed “discrete time crystal”. Interestingly, some of our work showed that time crystals are not limited to the quantum domain, but can also arise in well-established models of epidemic spreading on small-world graphs [18].

Continuing the idea of classical versions of something quantum, we also demonstrated by example that behaviour usually associated to quantum chaotic behaviour (linear growth of entanglement to volume law, a measurement induced phase transition to area law) also appears in classical circuits [19].